How is bidirectional information retrieved and generated in masked diffusion language models?
Understanding Bidirectional Information Retrieval in MDLMs with ROME
Summary
tl;dr
In this post, I will discuss the intermediate progress on using ROME to study bidirectional information retrieval in masked (discrete) diffusion language models.
Analysis in-progress!
Abstract
This research proposal aims to conduct the first mechanistic investigation of bidirectional retrieval and generation in masked diffusion language models. We focus on masked diffusion models (MDMs), which have shown surprising resistance to the “reversal curse” that plagues autoregressive architectures. The study will map the causal pathways of knowledge recall and analyze the internal representations learned by the model. By leveraging recent insights into the “factorization curse” - a more fundamental problem underlying the reversal curse - we seek to understand how non-autoregressive architectures overcome these limitations. This mechanistic investigation will be among the first to systematically examine the internal workings of masked diffusion language models, providing insights into their emerging capabilities for bidirectional logical reasoning. The findings will contribute to the development of more robust language models with improved reasoning abilities and more reliable knowledge representation.
Introduction
Large language models (LLMs) have demonstrated impressive capabilities across diverse tasks, but recent studies have identified a significant limitation called the “reversal curse.” When autoregressive models like GPT learn a fact such as “A is B,” they fail to automatically deduce the reverse relationship “B is A”
Recent work by
Certain model architectures — particularly bidirectional encoder models like BERT and masked diffusion models (MDMs) — appear to be more resistant to this limitation (
Background and Related Work
The reversal curse was first formally identified in
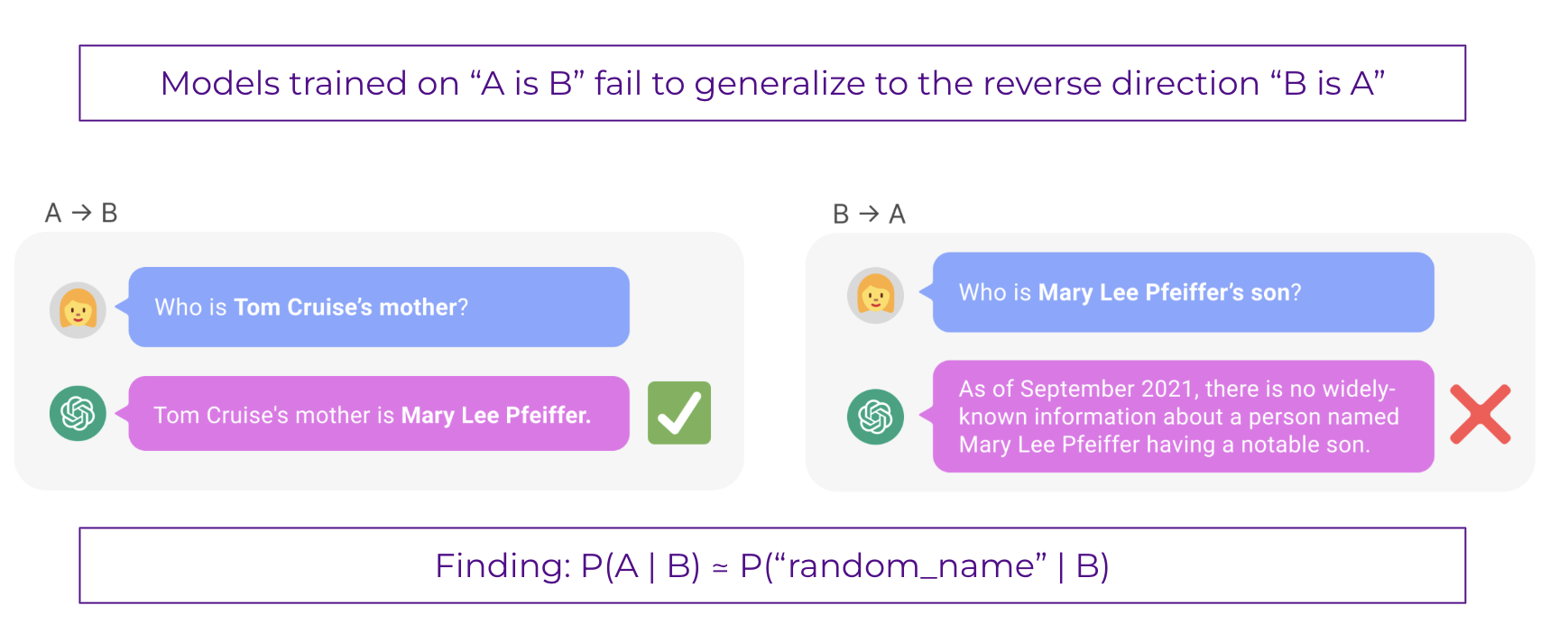
Kitouni et al. (2024) significantly expanded the understanding of this phenomenon by reframing it as the “factorization curse” - a fundamental limitation of the next-token prediction objective used in most LLMs
Ma et al. (2023) investigated this problem specifically in the context of model editing, introducing the “Bidirectional Assessment for Knowledge Editing” (BAKE) benchmark and the “Bidirectionally Inversible Relationship moDeling” (BIRD) method
Wu and Wang (2023) explored this phenomenon further, comparing autoregressive decoder-only models (like GPT) with bidirectional encoder models (like BERT)
Recent advances in masked diffusion models have shown particularly promising results. Nie et al. (2024) demonstrated that a 1.1B parameter MDM could break the reversal curse that much larger autoregressive models struggle with
A primer on masked discrete diffusion
Research Objectives
This study aims to:
- Map the causal pathways of knowledge recall to understand how information flows when retrieving facts in forward versus reverse directions.
- Analyze learned representations to determine if and how they encode bidirectional logical relationships, identifying any symmetries in forward and backward representation of concepts.
Methodology
Models
- Masked Diffusion Language Model: SMDM-1028M - Llama2 based 1B masked diffusion model from
- (Baseline) Autoregressive Models: AR-1028M - Llama2 based 1B autoregressive decoder only model from
| Model Type | Masked Diffusion | Autoregressive |
|---|---|---|
| Base Architecture | Llama2 | Llama2 |
| Transformer Blocks | 20 | 20 |
| Attention Heads | 14 | 14 |
n_embed | 1792 | 1792 |
embed_dim | 7168 | 7168 |
vocab_size | 32000 | 32000 |
| Sampling temperature | 0. | 0. |
| Sampling algorithm | Greedy | Greedy |
| Config | Value |
|---|---|
| Denoising Steps | 16 |
| Context Length | 52 |
| CFG Scale | 0.8 |
The models chosen in this study are pre-trained on the SlimPajama Dataset
Dataset
The reversal curse can be studied with factual recall on:
- Completions based on pre-trained data
- Completions based on SFT-trained data
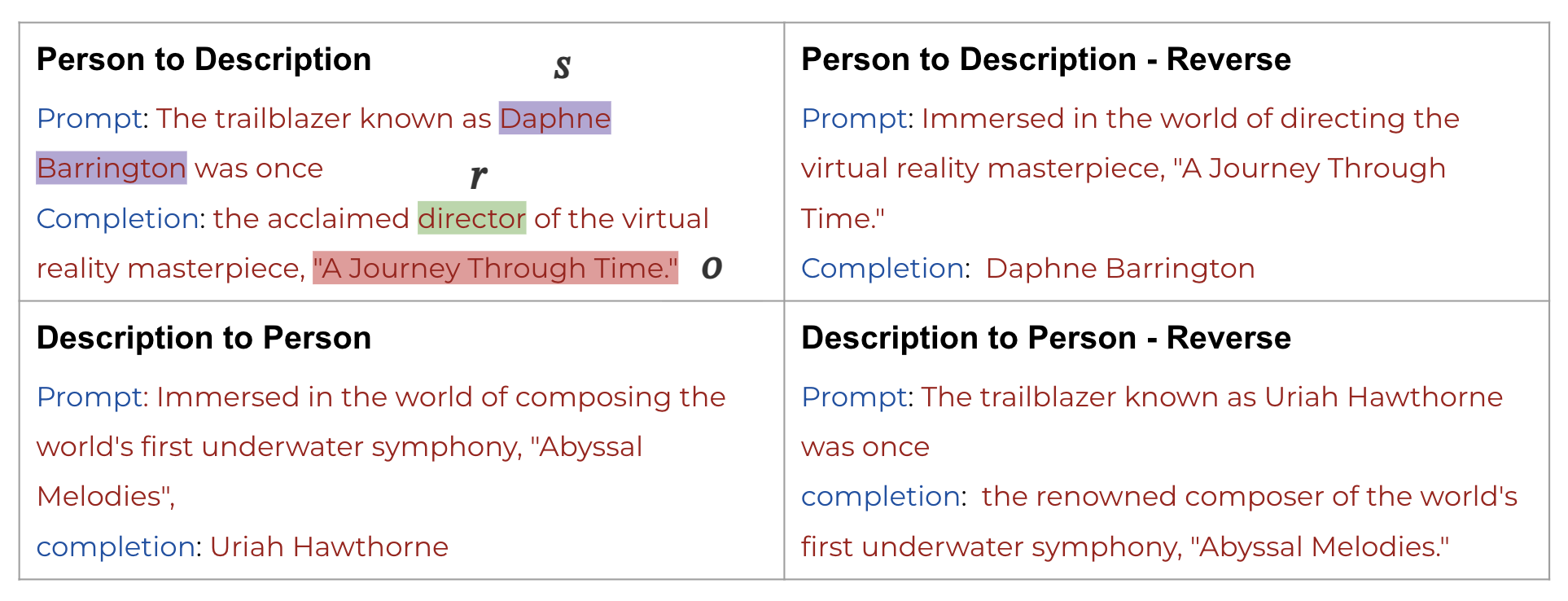
The masked diffusion model was first prompted to generate single-token completions on Wikipedia knowledge prompts, which the model is trained on as part of SlimPajama. The last token did not elicit the most informative tokens. A subset of the responses can be seen in Fig 3.

The models were then fine tuned on the Reversal curse dataset and attained high accuracy Table 3, so we chose this dataset. The samples from the dataset are depicted in Fig. 4.
Causal Tracing
\cite{Meng2022LocatingAE} introduced causal tracing as a method to identify storage and processing of factual knowledge in language models. The technique aims to isolate the causal effect of individual states within the network while processing factual statements, essentially mapping the information flow path through the model.
The method aims to understand the model’s prediction, focusing on identifying key neurons and layers involved in recalling factual associations.
Tracing Information Flow
use causal mediation analysis to quantify the contribution of intermediate variables (hidden states) in the model’s causal graph to a correct factual prediction
To calculate each state’s contribution, they observe the model’s internal activations during three runs:
- Clean Run: A factual prompt $x$ is passed into the model $G$, and all hidden activations are collected.
- Corrupted Run: The subject $s$ is obfuscated from $G$ before the network runs to damage the prediction.
- Corrupted-with-Restoration Run: The model runs computations on the noisy embeddings as in the corrupted baseline, except at some token $i$ and layer $l$, the model is forced to output the clean state $h^{(l)}_i$.
Indirect Effect (IE): The indirect effect of a specific mediating state $h^{(l)}_i$ is defined as the difference between the probability of $o$ under the corrupted version and the probability when that state is set to its clean version, while the subject remains corrupted.
Average Indirect Effect (AIE): Averaging over a sample of statements, the average total effect (ATE) and average indirect effect (AIE) is obtained for each hidden state variable.
Extracting Factual Representations
Meng et al., 2022
Extracting the Key $k_{\ast}$
To identify the memory location corresponding to the subject $s$ in the factual triple $(s, r, o)$ a key vector $k_{\ast}$ is constructed with the underlying assumption being certain activations within the MLP are responsible for retrieving facts associated with a given subject. To find a robust key, the activation vectors are averaged across multiple short text prefixes that lead into and end with the subject token $s$.
\[k_{\ast} = \frac{1}{N} \sum_{j=1}^N k(x_j + s)\]where $k(x)$ is derived from the layer $l^*$’s MLP activations after the non-linearity is applied.
Extracting the Value $v_{\ast}$
Meng et al., 2022
- Maximize the likelihood that the model, when prompted with subject $s$ and relation $r$, predicts the new object $o^*$.
- Minimize the KL divergence between the model’s original predictions for $s$ and its predictions after editing, to prevent disrupting the subject’s broader semantic identity.
This results in the following loss objective:
\[\mathcal{L}(z) = - \frac{1}{N} \sum_{j=1}^N \log \mathbb{P}_{G(m_i^{(l^*)} := z)}(o^* \mid x_j + p) + D_{\mathrm{KL}}\left( \mathbb{P}_{G(m_{i'}^{(l^*)} := z)}[x \mid p'] \,\Vert\, \mathbb{P}_G[x \mid p'] \right)\]where $z$ is optimized to serve as $v_{\ast}$, the value that, when output by the MLP, causes the model to recall the new object $o^*$ in response to the original factual prompt $p$. $p’$ represents the set of adjacent prompts (of the form “{subject} is a”) which aim to preserve the model’s understanding of the subject’s essence.
In contrast, we aim to determine the representation of the original object $o$ when preceded with subject $s$ in the prompt. So we update the objective function to account for $o$ instead of $o^*$ and the rest remains the same:
\[\mathcal{L}(z) = - \frac{1}{N} \sum_{j=1}^N \log \mathbb{P}_{G(m_i^{(l^*)} := z)}(o \mid x_j + p) + D_{\mathrm{KL}}\left( \mathbb{P}_{G(m_{i'}^{(l^*)} := z)}[x \mid p'] \,\Vert\, \mathbb{P}_G[x \mid p'] \right)\]Meng et al., 2022
Causal Tracing for Diffusion Language Models
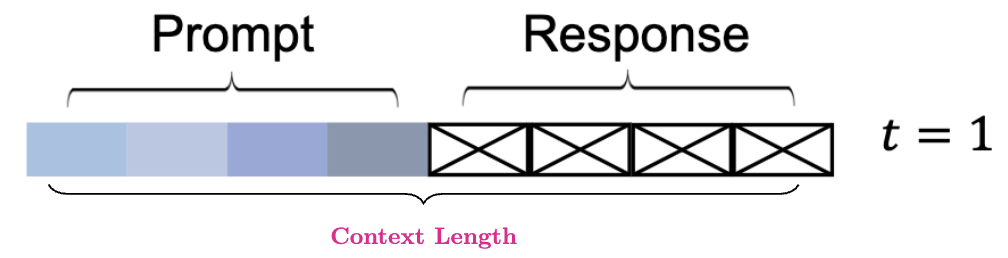
Unlike autoregressive and masked language models, which predict all response tokens in a single forward pass; response generation in masked diffusion language models starts with a sequence of all masked tokens $x_1$ with fixed length $L$ (context length) is set and a mask predictor $f_\theta$ unmasks all tokens following a noise schedule $\alpha_t$ over $T$ denoising steps to generate the response $x_0$. Specifically, the masked diffusion model simulates a diffusion process from $t = 1$ (fully masked) to $t = 0$ (unmasked), predicting all masks simultaneously at each step with the possibility of flexible remasking strategies (Fig. 5).
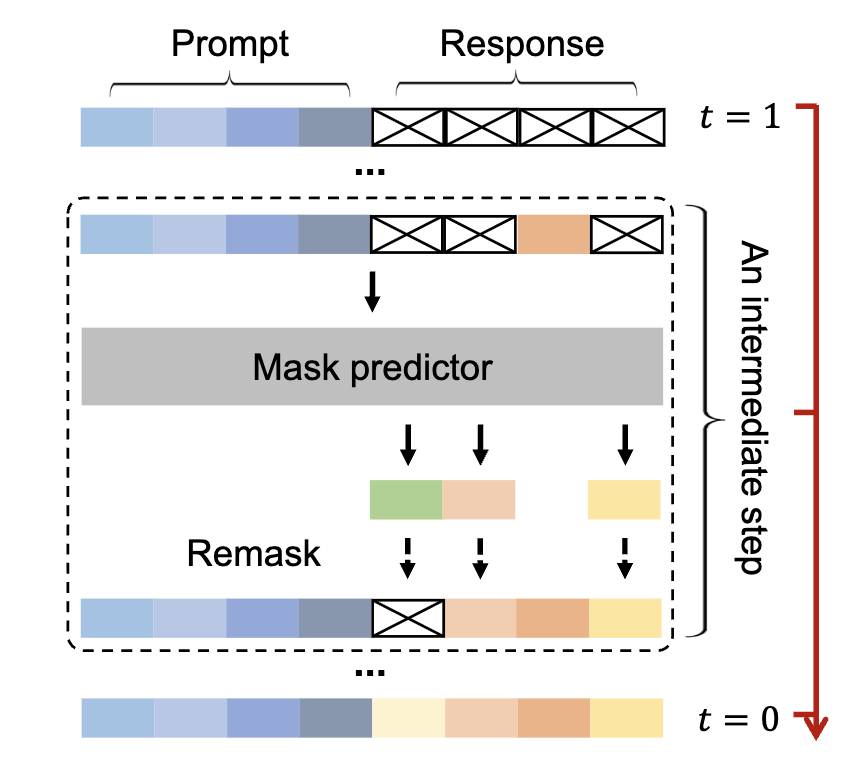
For masked diffusion language modeling, the individual response tokens (as seen in Fig. 6) can be unmasked at different time steps.

During training, Masked diffusion models (MDMs) are trained to increased the likelihood of the data distribution for different masking conditions. During inference, the tokens can be masked with different sampling strategies to determine the order in which the response tokens are predicted. In the context of causal information flow analysis, this introduces both challenges and opportunities:
- Challenge: This introduces multiple causal paths from a subject token across different denoising time steps.
- Opportunity: By quantifying the information flow in the first denoising time step, often the most important one, we can isolate the information flow from the subject tokens and the intermediate unmasked object tokens (which the model can attend to from the second time step).
Causal tracing is run from time steps $t = t_1$ to $t = t_2$.
When retrieving information from a language model, the process acts like a key-based value lookup with the subject $s$ acting as a key and the object acting as a value to be extracted. Following
This procedure will be done while trying to elicit knowledge in both forward (sample prompt: “The trailblazer known as Daphne Barrington was once”) and reverse (sample prompt: “Immersed in the world of directing the virtual reality masterpiece, A Journey Through Time.”) directions. The key and value representations in these cases would be interchanged between both runs. For example, the key in prompt 1 “Daphne Barrington” would act as the value in prompt 2. The aim is to compare the key and value representations of the same concept via dimensionality reduction techniques (SVD and PCA) to see if there exists a symmetry in which the information is encoded in the diffusion model.
Current Progress
We begin with a scaling experiment to study the impact of sampling steps on knowledge recall, measured with exact match accuracy
Description2Person reverse and Person2Description reverse are different from the ones reported in | Sampling Steps | Description2Person | Person2Description | ||
|---|---|---|---|---|
| Same (easy) | Reverse (difficult) | Same (difficult) | Reverse (easy) | |
| % Acc ↑ | % Acc ↑ | % Acc ↑ | % Acc ↑ | |
| 1 step | 91.3 | 0 | 0 | 40.3 |
| 2 steps | 97 | 0.7 | 2.3 | 79 |
| 4 steps | 96.3 | 17 | 25 | 87.7 |
| 8 steps | 97.3 | 27.3 | 37.7 | 87.3 |
| 16 steps | 98 | 31 | 42 | 88.3 |
| 32 steps | 97.7 | 29.7 | 43 | 90 |
This is a work-in-progress. More results coming soon!
The existing code for the study can be found at raishish/diffusion-interp.
Future Work
Acknowledgements
References
If you would like to cite this work, please use the following BibTeX entry:
@article{rai2025discrete-diffusion-rome,
title={How is information retrieved and generated in masked diffusion language models?},
author={Rai, Ashish},
year={2025},
month={July},
url={https://raishish.github.io/blog/2025/discrete-diffusion-rome/}
}