Characterizing arithmetic length generalization performance in large language models

An initial exploration of a mechanistic understanding of arithmetic performance (and performance scaling) in large language models.

Summary

tl;dr

We tested arithmetic capabilities of GPT-4o-mini, LLaMa-3.1-70B, LLaMa-3.1-8B, and Gemma-2b-it on increasingly complex numbers. While these models achieve very well (~94%) on GSM-8K, their performance degrades significantly with number complexity: addition works up to 6-digit numbers then fails, multiplication drops to 0% accuracy after 3-digit numbers, unique digit count matters more than number size (e.g., “48346” is harder than “480000”). Models consistently get first/last digits right even when overall answers are wrong, and mechanistic analysis shows final numerical answers emerge in later transformer layers.

Bottom line: Current LLMs have clear arithmetic boundaries that aren’t solved by scale alone.

Team

Team members: Ashish Rai, Akash Peddaputha, Aman Gupta

Advised by: Professor He He (as part of the NLP graduate level course at NYU, Fall 2024)

Full report (with additional results): link.

Research Approach

We designed a two-pronged approach to investigate this phenomenon:

  1. Standard Benchmark Testing: We first evaluated model performance by perturbing numerical values for questions in the GSM-8K dataset, a standard mathematical reasoning benchmark containing grade-school-level problems.

  2. Custom Dataset Creation: We then developed our own Arithmetic Length Generalization Dataset (ALGD) with 3,500 examples specifically designed to test scaling behavior across different operations:

    • Addition
    • Multiplication
    • Subtraction
    • Division
    • Modulus

For each operation, we created 100 examples with progressively more complex numbers, ranging from 1-digit to 7-digit values, allowing us to precisely identify where performance drops.

Key Discoveries

Baseline Performance

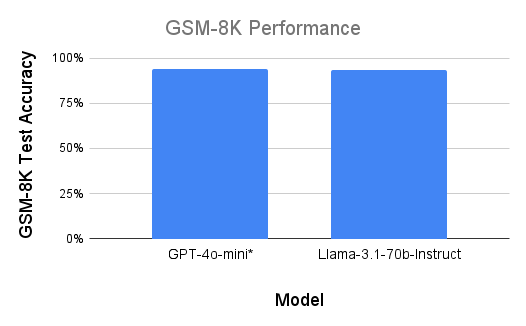
Our initial evaluation confirmed that frontier models perform impressively on standard mathematical reasoning tasks. Both GPT-4o-mini and LLaMa-3.1-70B-Instruct achieved approximately 94% accuracy on the unmodified GSM-8K dataset. This established a strong baseline for our subsequent experiments.

Length Generalization Patterns

When we increased numerical complexity, we observed fascinating patterns:

  1. Simple Scaling Works Well: When we multiplied values in GSM-8K problems by constants (like 1000), model performance remained strong. For example, models handled “48” and “480000” with similar accuracy.

  2. Unique Digits Matter More Than Size: The critical factor affecting performance wasn’t merely the size of numbers but their complexity in terms of unique digits. Models struggled significantly with smaller numbers containing more diverse digits (like “48346”) compared to larger but simpler numbers.

  3. Operation-Specific Thresholds: We identified clear performance thresholds for different operations:
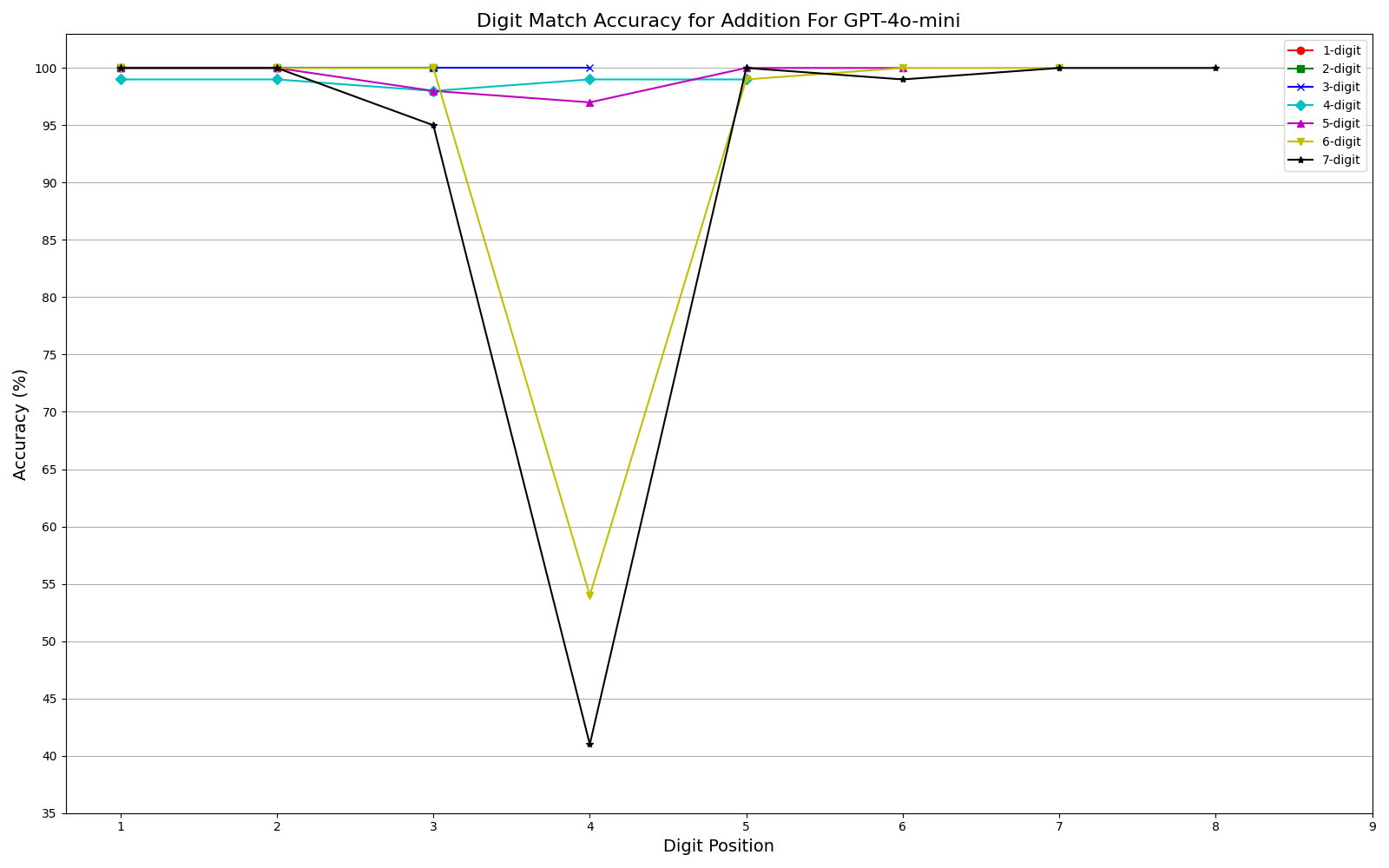
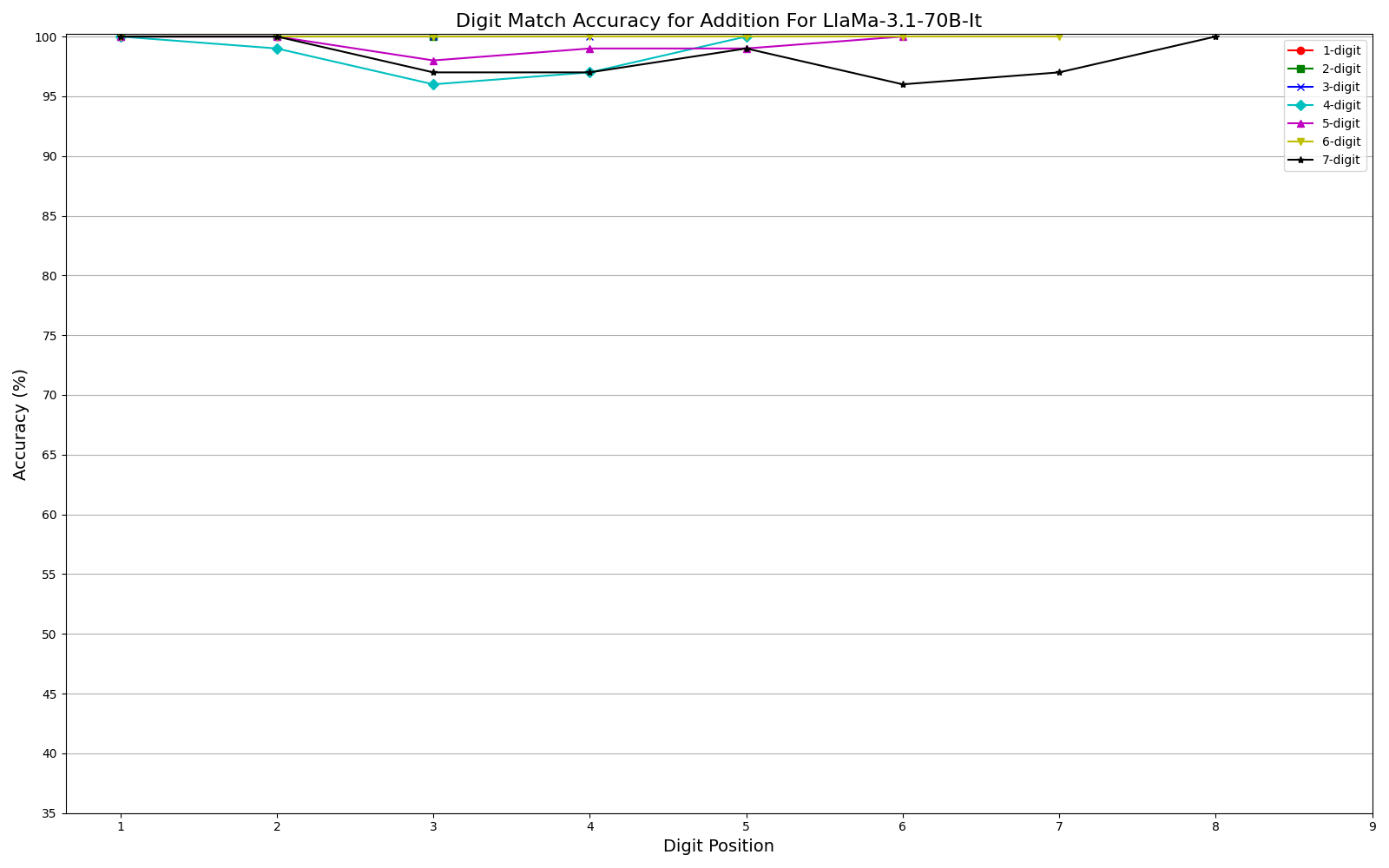
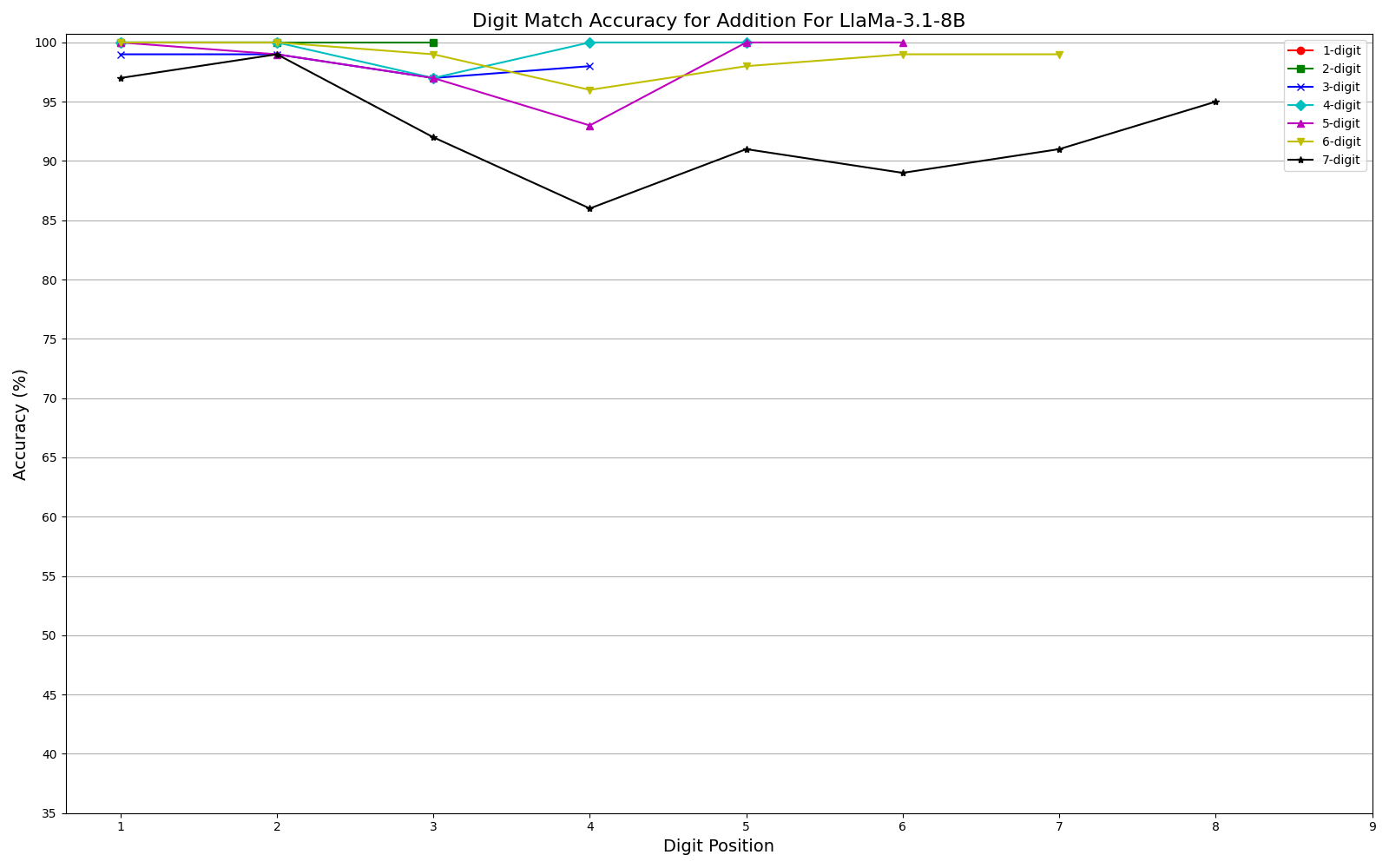
    • Addition: Models generally maintained accuracy up to 6-digit numbers
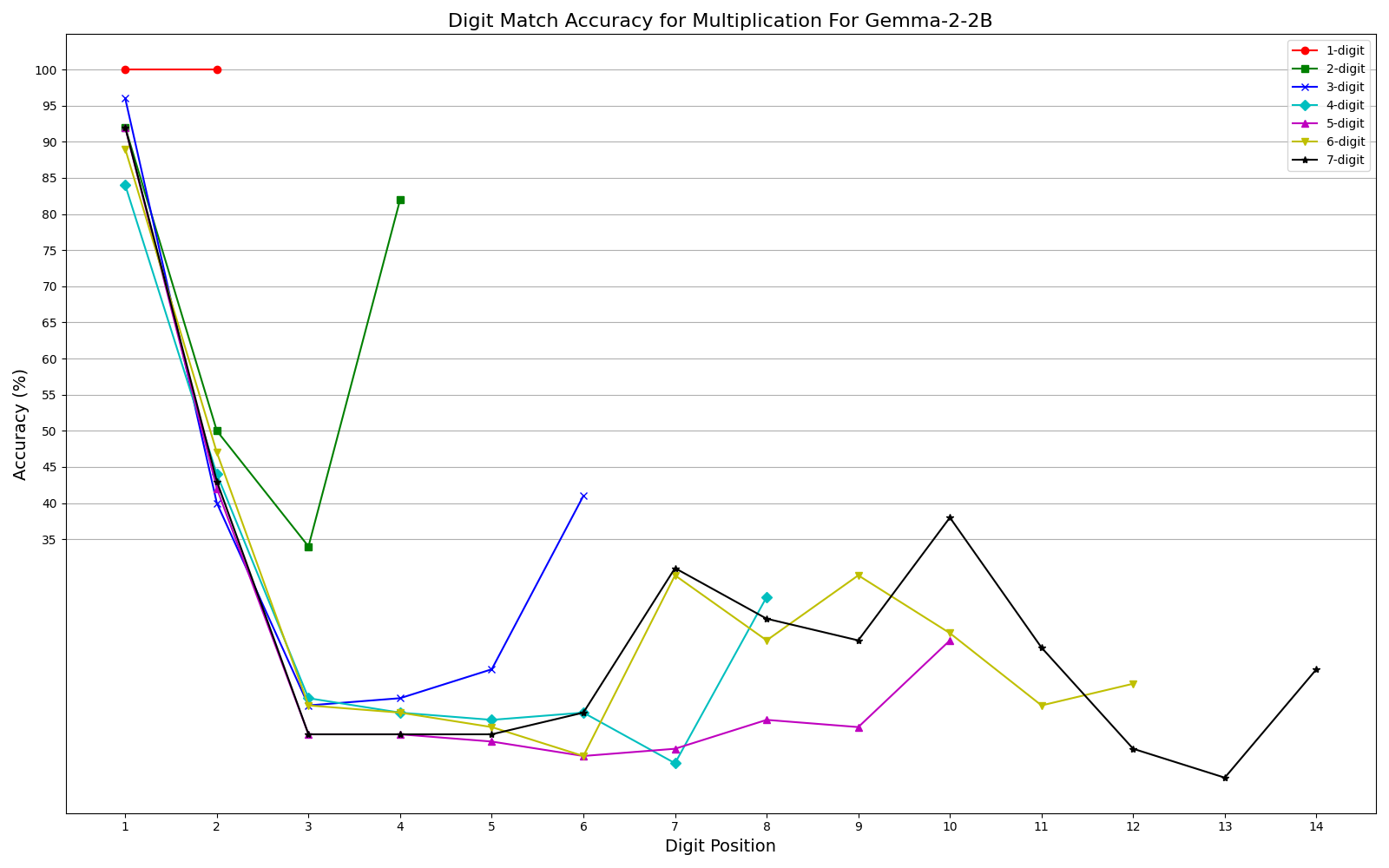
    • Multiplication: Performance declined sharply after 3-digit numbers, reaching 0% for larger values
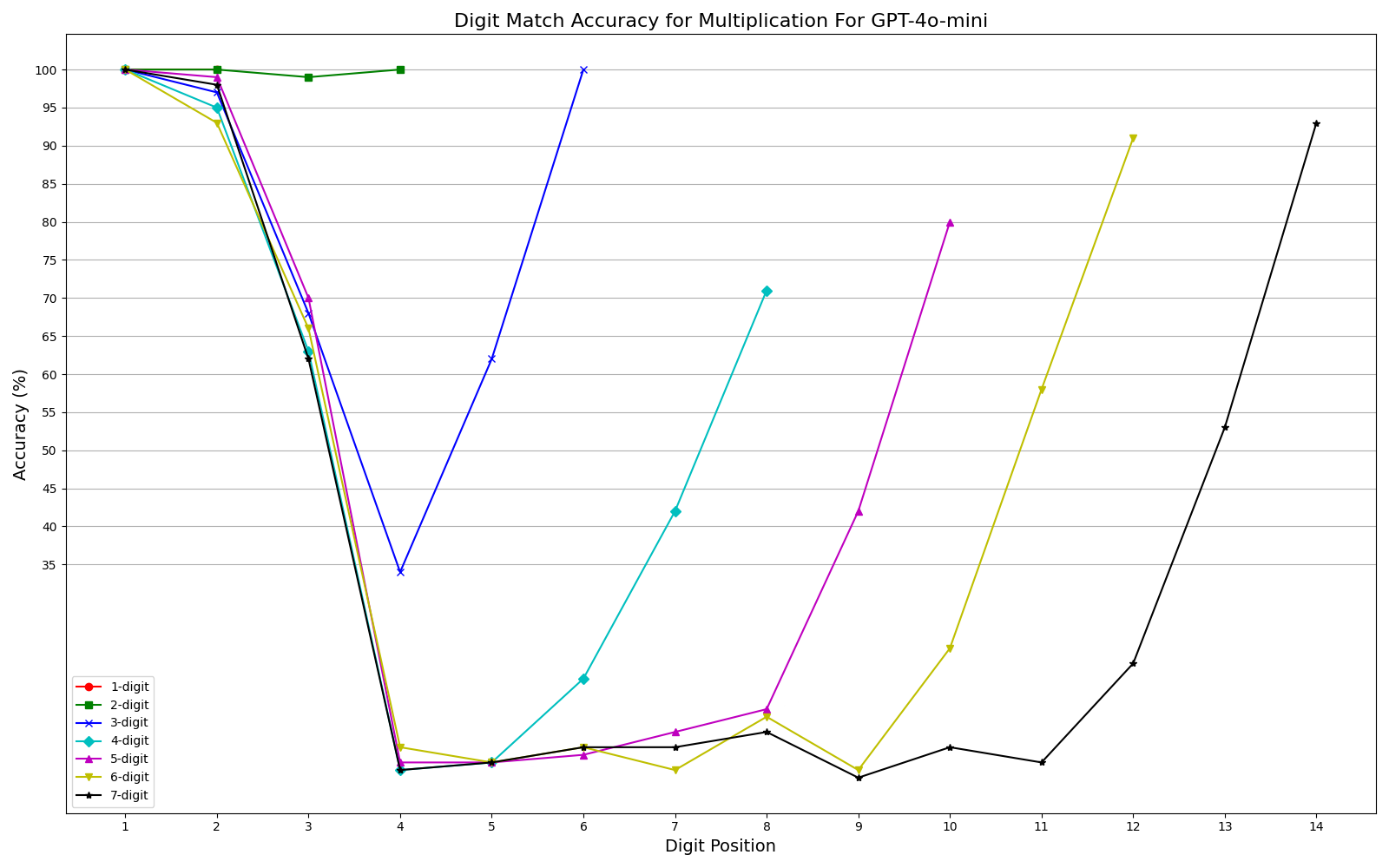
  4. Edge Digits vs. Middle Digits: One particularly interesting finding was that models tended to get the first and last few digits correct even when overall accuracy declined. The middle digits showed consistently higher error rates.

Mechanistic Insights

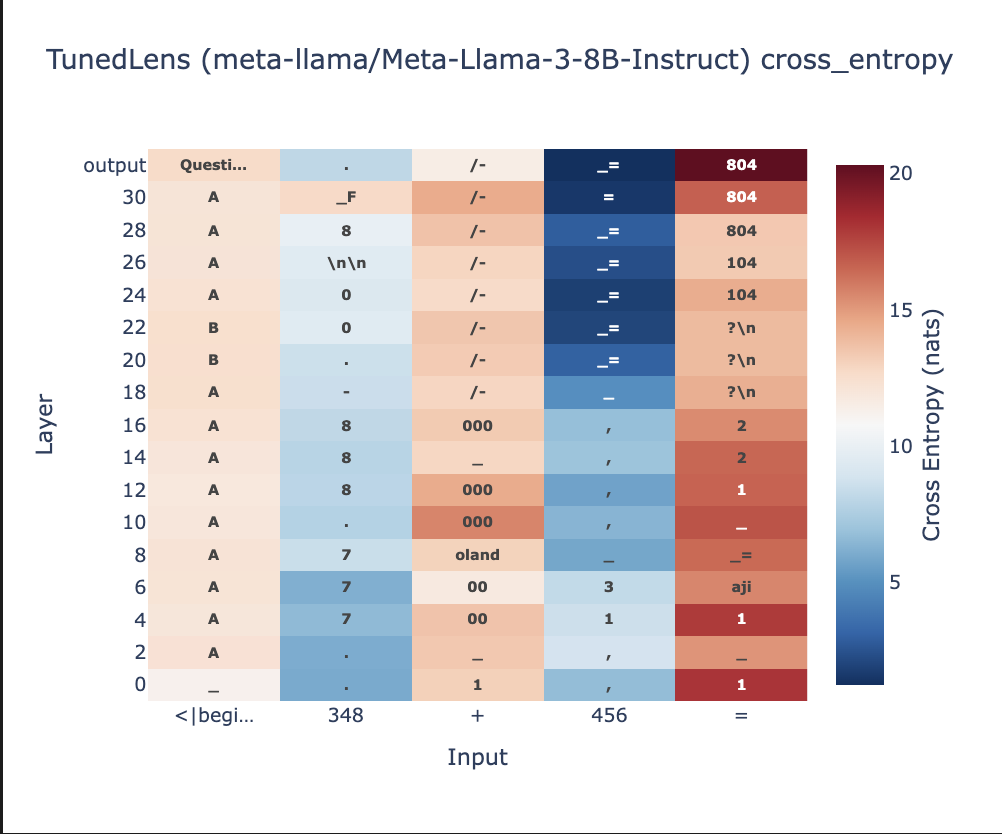
Using interpretability techniques like Tuned Lens (built upon Logit Lens), we examined how responses are generated at different layers of the network. Our analysis revealed:

  1. The final numerical answers are primarily generated in the later layers of the model
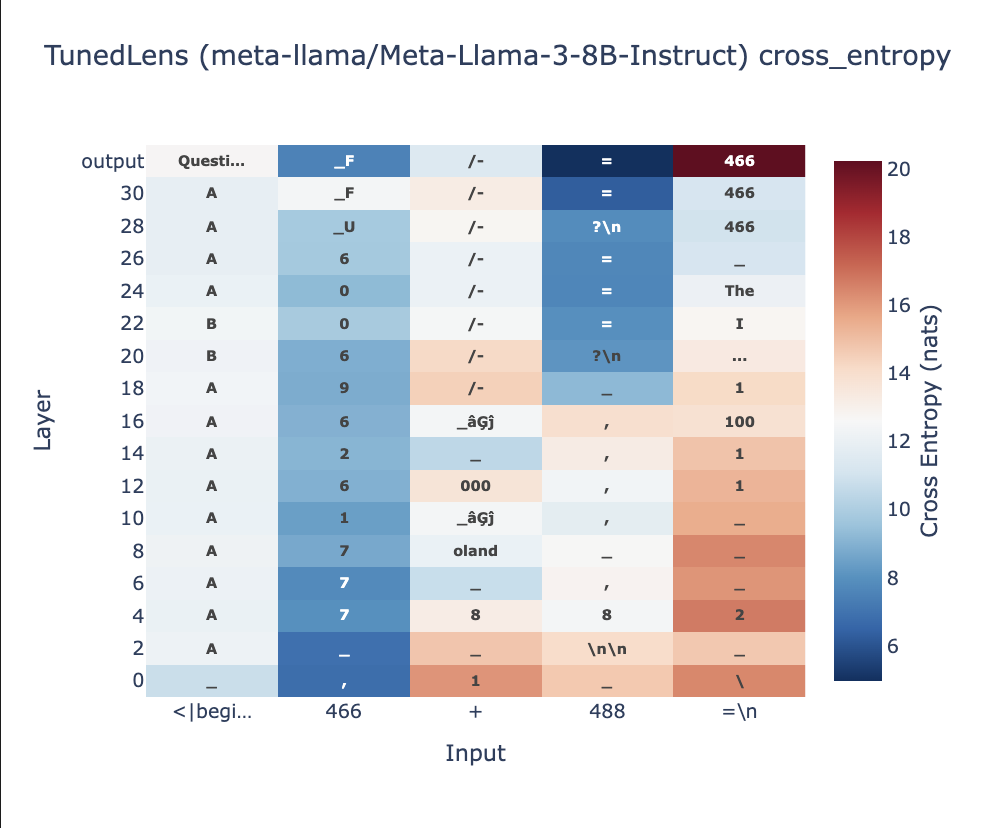
  2. Even when providing the first token of multi-token answers in the prompt, models frequently failed to generate subsequent tokens correctly.

Implications and Future Directions

Our findings highlight important limitations in current LLMs’ arithmetic capabilities. While these models excel at numerous language tasks and can handle basic calculations, they demonstrate clear boundaries in their ability to process complex numerical operations.

As researchers, we’re now focused on:

  1. Mechanistic Understanding: Using white-box experiments to analyze why these limitations occur
  2. Intermediate Decoding: Examining model outputs at different stages to identify where errors emerge
  3. Component Analysis: Identifying specific architectural elements that influence arithmetic performance

Our goal isn’t necessarily to improve arithmetic operations in LLMs (specialized tools already exist for this purpose) but rather to understand how numerical complexity affects model behavior and reasoning.

Abstract

Large language models (LLMs) excel at single-pass NLP tasks like text generation, but struggle with unbounded multistep computations like arithmetic operations with large numbers. This study aims to assess and formulate the length generalization of arithmetic reasoning of LLMs. We observed a significant degradation in model performance when the questions were rephrased with the numerical values scaled in length when tested on the GSM-8K benchmark. We further investigated the scaling behavior on arithmetic tasks and found that state-of-the-art models like GPT-4o-mini and LLaMa-3.1-70B can generate accurate outputs for 4-digit addition and 3-digit multiplication. However, accuracy declines sharply with larger numbers, particularly when the number of unique digits increases. Our results show that while models can generally handle the addition of numbers containing 6 digits and multiplication of 3-digit numbers, they often fail for higher orders. Despite errors on higher-order numbers, we observe a pattern in digit-wise accuracy: the first and the last few digits have higher accuracy than those in the middle, highlighting specific numerical limits in LLM’s capabilities for arithmetic tasks. The dataset is uploaded to Hugging Face and the code for reproduction are publicly available at https://github.com/raishish/arithmetic-interp.

Introduction

Large Language Models (LLMs) have shown remarkable prowess in various domains, such as natural language processing, question answering, and creative tasks . Nevertheless, they still face challenges when it comes to arithmetic operations. Solving math problems necessitates a combination of skills, including text comprehension and arithmetic calculation . Research indicates that the reasoning process employed by LLMs is often based on probabilistic pattern-matching rather than formal logical reasoning .

Recent studies on Transformers indicate that models specifically trained on addition and other arithmetic tasks encounter difficulties in generalizing to varying lengths and complexities of numbers . Even when fine-tuned from pre-trained LLMs, these models continue to struggle with fundamental algorithmic tasks, highlighting the disparity in their capacity to effectively handle numeric complexity .

LLMs excel in text generation and summarization, but upon closer examination their limitations in mathematical reasoning capabilities become apparent. In this project, we systematically investigate the arithmetic reasoning of LLMs by examining their generalization performance on elementary arithmetic tasks. We modify numerical values in the GSM-8K benchmark to assess the sensitivity of models like GPT-4o-mini and LLaMa-3.1-70b-Instruct to increasing numerical complexity. Additionally, we explore the scaling behavior of LLMs on these tasks by gradually increasing the complexity of numerical values, testing their accuracy on elementary arithmeric operations from 1-digit to 7-digit numbers. Our experiments show that LLMs can handle simpler arithmetic tasks but their accuracy deteriorates with increasing complexity, especially for smaller numbers with higher unique digit counts.

Through this study, we aim to understand the impact of numerical complexity and arithmetic operations on the scaling behavior of LLMs, rather than improving arithmetic operations.

Recent advances in LLMs have spurred interest in improving their mathematical reasoning capabilities. introduces GSM-Symbolic, an improved benchmark to evaluate LLMs on math reasoning tasks. Their approach reveals the fragility of LLM reasoning, with model performance sensitive to slight numerical changes. further explores LLM reasoning mechanisms by identifying critical attention heads and MLPs essential for arithmetic calculations.

The work in addresses scaling behavior of LLMs across numeral systems, comparing base-10 and base-100 tokenization schemes. provides a survey on LLMs in mathematical reasoning, categorizing problem types and identifying relevant datasets for arithmetic, geometry, and theorem proving. Finally, the work by investigates transformers’ length generalization capabilities. It focuses on transformer architectural aspects that affect their generalization on length-variable tasks.

Our approach builds on these works by analyzing the effects of symbolic reasoning templates and tokenization schemes on mathematical problem-solving accuracy, providing an extended evaluation across larger datasets.

Approach

We evaluated the model’s performance on the GSM-8K dataset by multiplying numerical values by multiples of 10, which did not increase the complexity much since the number of unique digits remains constant. The model consistently produced correct answers for such questions. To further increase complexity, we introduced random numbers with more unique digits and tested the model’s handling of these variations. We also used one-shot and few-shot and Chain of Thought (CoT) prompting to improve multi-step reasoning. The models were prompted to not use or generate code to generate responses, thus avoiding the impact of code interpreting techniques. We experimented with different sampling settings and conducted repeated tests under similar conditions to ensure consistency.

To mechanistically understand how responses are generated for arithmetic operations, we use transformer interpretability techniques to look for attribution of intermediate layers of the network to the final response.

Experiments

Data

In this work, we evaluate our models using two datasets: the widely-used GSM-8K test dataset and a custom dataset we created for evaluating length generalization of arithmetic performance. For both datasets, the task involves generating an accurate numerical output in response to the arithmetic input or question.

GSM-8K Dataset

For evaluating our models’ mathematical reasoning capabilities, we use the GSM-8K dataset . GSM-8K contains grade-school-level math problems designed to assess logical reasoning and arithmetic capabilities in large language models (LLMs).

Arithmetic Length Generalization Dataset (ALGD)

To evaluate our model’s performance on elementary arithmetic operations, we designed a custom dataset with 3,500 examples for addition, multiplication, subtraction, division, and modulus. Each operation includes 100 examples with 1-digit to 7-digit numbers (~around 700 per operation), allowing us to assess the model’s capacity to handle progressively more complex scenarios.

Evaluation methodology

We assess the model’s arithmetic reasoning using accuracy metric on the GSM-8K and ALGD datasets. For GSM-8K, accuracy measures the percentage of correctly answered questions, benchmarking general mathematical reasoning and comparing with prior work. On ALGD, we measure digit-wise accuracy separately across digit complexities for all operations, evaluating the model’s scalability and robustness with numerical complexity along with overall accuracy. This comprehensive approach highlights the model’s strengths and limitations in diverse mathematical tasks.

Experiment details

We use the configurations defined in Table 1 to evaluate GPT-4o-mini, Llama-3.1-70b-Instruct, Llama-3.1-8b-Instruct, and gemma-2b-it on both GSM-8K and ALGD datasets. We explicitly specify in the system prompt to not use any code to avoid GPT-4o-mini from using its Code Interpreter feature. The exact prompt for different models is shown below. We first compare the performance of both models on GSM-8K to establish a baseline. Inspired by GSM-Symbolic , we then increased the number of digits to increase the complexity of the questions and to move away from the training distribution. Finally, we evaluate the models on our generated ALGD dataset. We use Tuned Lens , built upon the Logit Lens approach, to project the activations from intermediate layers of Llama-3.1-8B-Instruct into the model’s vocabulary space. Tuned Lens helps avoid misalignment observed in Logit Lens due to evolution of representations by learning layer-specific probes to minimize the distribution shift.

Table 1: Model configuration parameters used in experiments.
Parameter Description Value
max_completion_tokens Max # of completion tks including output and reasoning tks 512
temperature Sampling temperature 0.7
top_p Probability mass to sample tokens from 0.9
$n$ # of sequences generated 1
seed Seed for random number generator 0 
# GPT-4o-mini prompt
messages =[
  {
    "role": "system",
    "content": "You are a helpful assistant. Do not use or generate code in your responses. Please respond with only the final answer, formatted as a single number without additional explanation or context."},
  {
    "role": "user",
    "content": f"{query} \n\nPlease provide only the final answer as a single number."
  }
]

# Prompt for Llama and Gemma models
messages =[
  {
    "role": "system" ,
    "content": "You are a helpful assistant. Do not use or generate code in your responses . Also append the final numerical answer on a new line append with '#### '" } ,
  {
    "role": "user",
    "content": f"{query}"
  }
]

Results

It can be seen from Fig. 1 that frontier models perform with $\sim$94% accuracy on the GSM-8K dataset. However, when the number of digits in the numerical values are increased, our observations reveal that models perform well with numbers containing fewer unique digits, such as 480000, but their accuracy declines with numbers that have more unique digits, even on a small scale (e.g., 48346) (Refer Appendix 6.2.3 in the report). Additionally, the models often misrepresent high-magnitude numbers, sometimes interpreting quadrillions as billions or using inconsistent scientific notation. As numeric complexity increases, models occasionally “hallucinate” numbers, particularly in responses to simple arithmetic prompts involving large sums. When using Few-Shot prompting, models show an over-fitting tendency to the set number of reasoning steps, producing accurate intermediate calculations but failing to combine these results correctly in the final answer. With Chain-of-Thought prompting, while models can decompose the operation between large numbers into those with smaller numbers and generate accurate results, they struggle with summing these intermediate results accurately.

Performance of SoTA models on GSM-8K
Figure 1: Frontier models like GPT-4o-mini and Llama-3.1-70b-Instruct score >90% on mathematical reasoning datasets like GSM-8K. *Due to the constraint max_completion_tokens set to 512, 6 out of 1319 responses by GPT-4o-mini were truncated. Accuracy is calculated after removing these question-answer pairs.
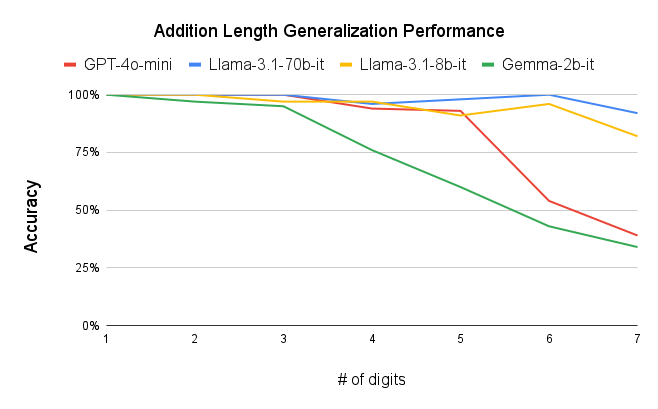
Addition Length Generalization Performance
Figure 2a: Performance deteriorates with increase in number of digits. Llama-3.1-70b-Instruct performs better than GPT-4o-mini whose performance drops after 5-digit addition.
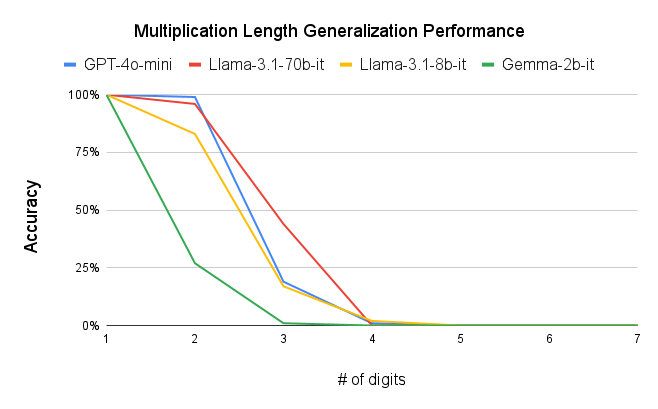
Multiplication Length Generalization Performance
Figure 2b: Performance of both Llama-3.1-70b-Instruct and GPT-4o-mini reaches 0% after 3-digit multiplication.

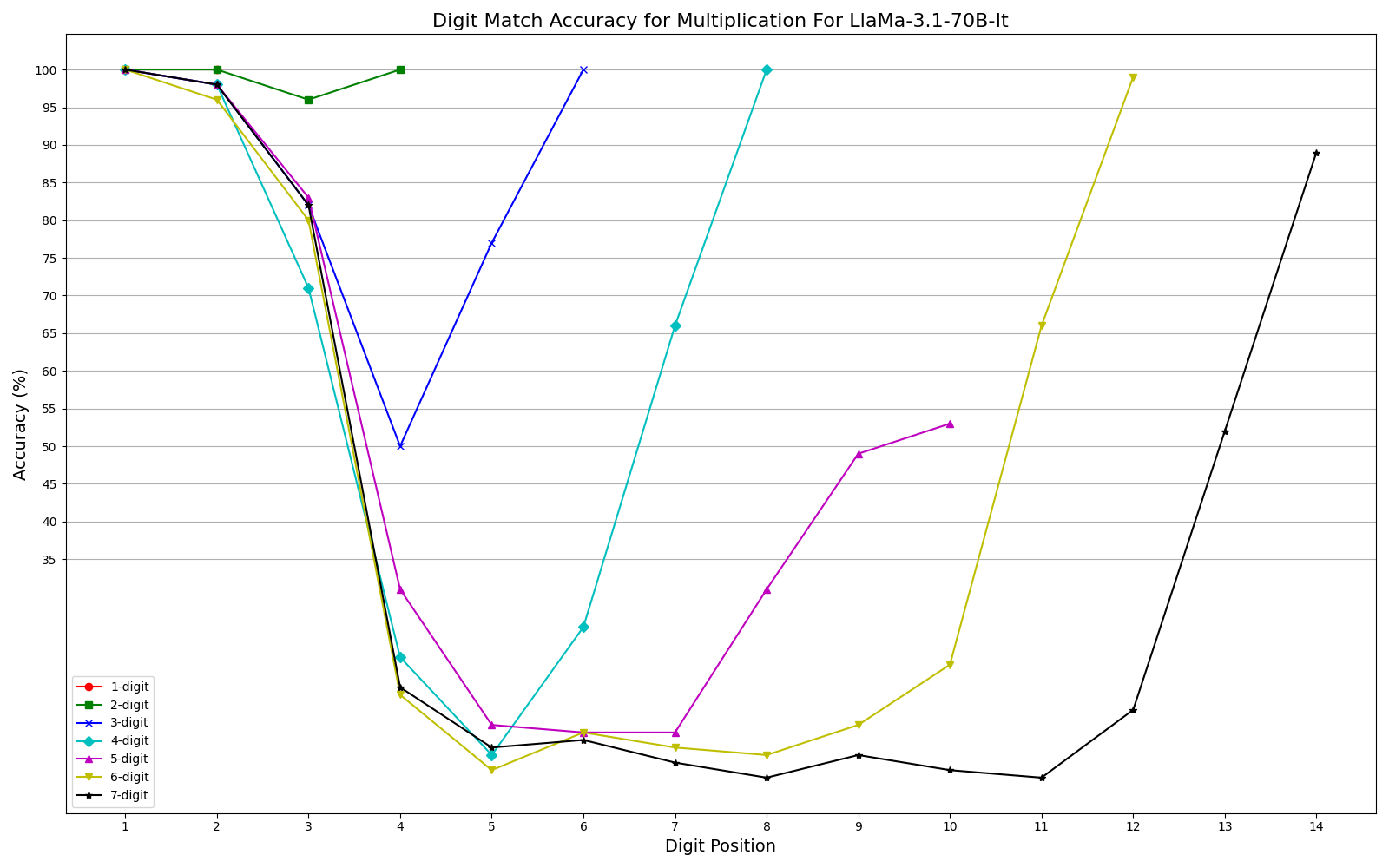
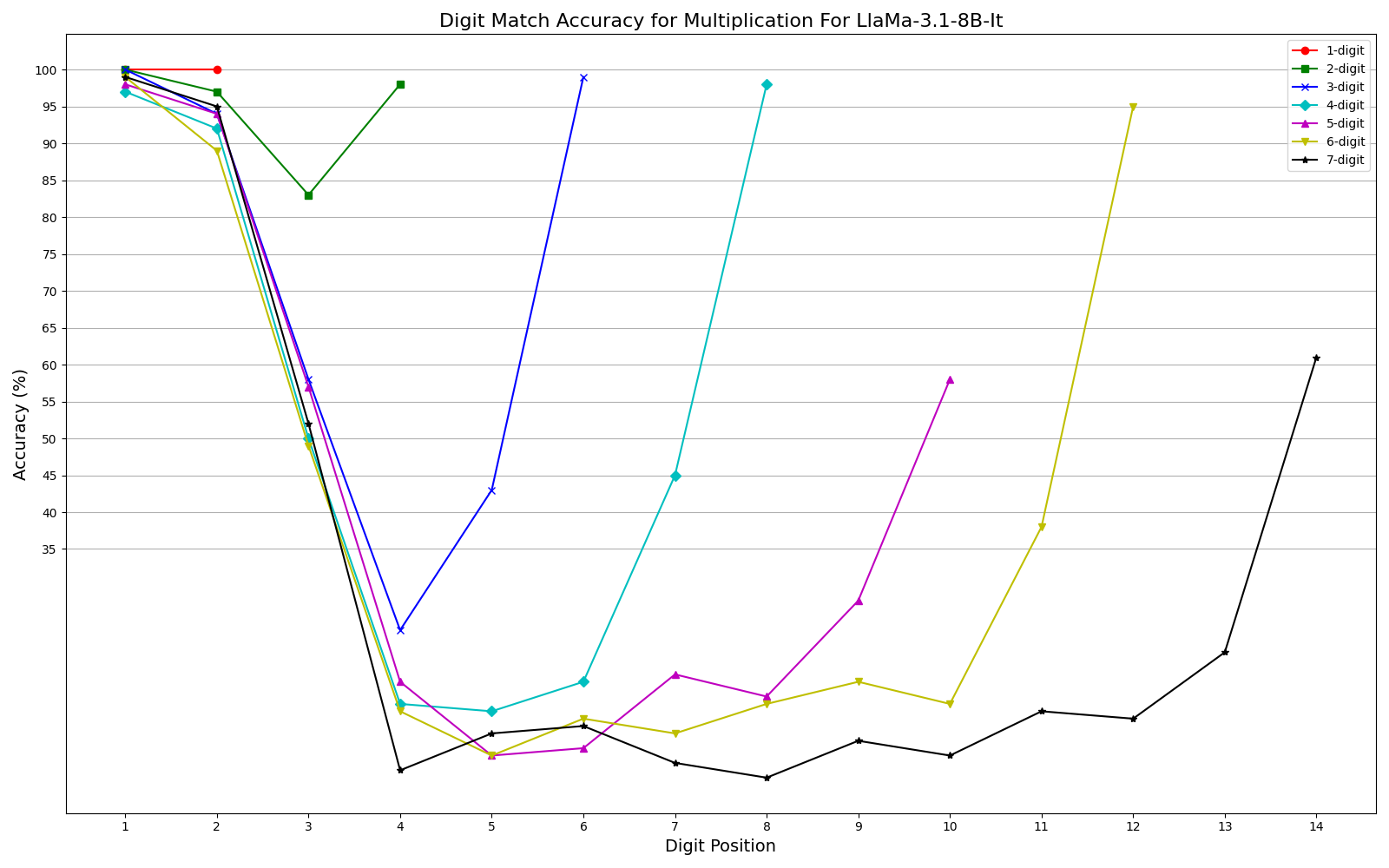
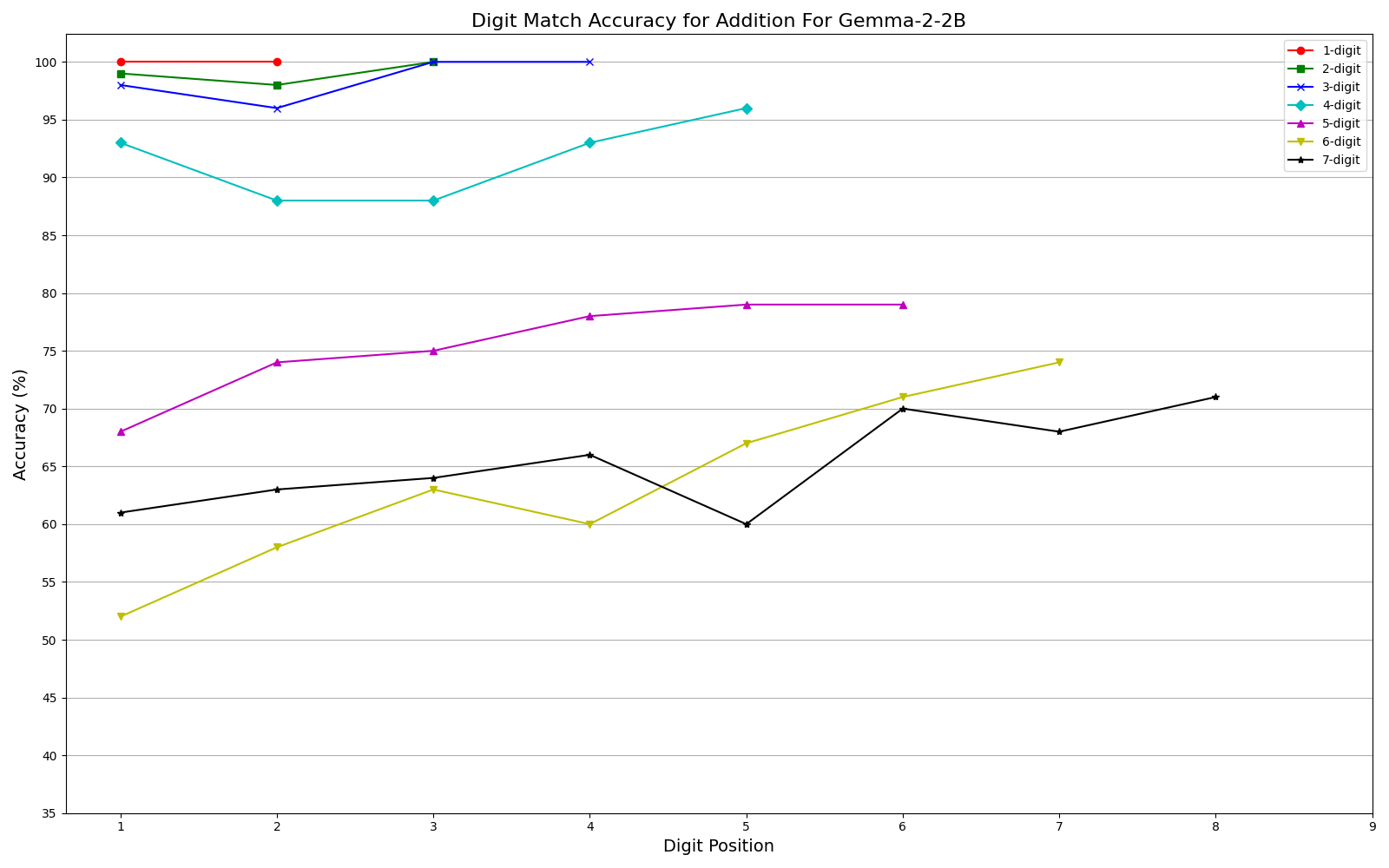
We observe performance of addition Fig. 2a and multiplication Fig. 2b limiting to 6-digit and 3-digit numbers, respectively, but exhibit significant errors beyond these limits. Furthermore, our results show that while models can generally handle computations involving numbers up to 6 digits, they often fail for higher orders, with larger unique digits in smaller numbers exacerbating error rates. One interesting observation is that, the models often generate the first and last few digits accurately, even as overall accuracy declines (Fig. 3a, Fig. 3b) . This could be related to frequencies of combination of specific digits in the training corpus or specific tokenization methods. More graphs can be seen in Appendix sections 6.3 and 6.4 in the report. We plan to explore further in this direction. The trend remains the same irrespective of different training recipes and tokenization strategies across the two models.

GPT-4o-mini 7-digit matches
Figure 3a: GPT-4o-mini digit accuracy.
Llama-3.1-70b 7-digit matches
Figure 3b: Llama-3.1-70b digit accuracy.

Figure 3: Digit accuracy for multiplication. The trend remains the same irrespective of different training recipes and tokenization strategies across the two models.

With tuned lens, it can be seen that the final numerical answer is generated in the later layers of Llama-3.1-8B Fig 4a. In case of multi-token answers, even after providing the first token in the prompt, the model fails to generate the next token Fig 4b.

GPT-4o-mini 7-digit matches
Figure 4a: Correct Response: TunedLens for Llama-3.1-8b-Instruct for 3-digit addition.
Llama-3.1-70b 7-digit matches
Figure 4b: Incorrect Response: TunedLens for Llama-3.1-8b-Instruct for 3-digit addition.

Figure 4: Tuned Lens Plots for Llama-3.1-8b-Instruct (Cross Entropy Loss).

More Multi-digit Multiplication Accuracy Graphs

Multiplication Length Generalization Performance
Multiplication Performance of Llama-3.1-8b-Instruct
Multiplication Length Generalization Performance
Multiplication Performance of Gemma-2-2b-Instruct

Multi-digit Addition Accuracy Graphs

Addition Length Generalization Performance
Addition Performance of GPT-4o-mini
Addition Length Generalization Performance
Addition Performance of Llama-3.1-70b-Instruct
Addition Length Generalization Performance
Addition Performance of Llama-3.1-8b-Instruct
Addition Length Generalization Performance
Addition Performance of Gemma-2-2b-Instruct

Conclusion

This research provides valuable insights into the current capabilities and limitations of LLMs in mathematical reasoning. While models like GPT-4o-mini and LLaMa-3.1-70B demonstrate impressive performance on standard benchmarks, they struggle with unbounded multistep computations involving complex numbers.

Understanding these limitations is crucial as we continue developing and deploying these models in real-world applications where mathematical reasoning may be required. Our findings contribute to the broader conversation about how to enhance and complement LLM capabilities in domains requiring precise numerical computation.

For those interested in exploring this further, our dataset and code are publicly available at our GitHub repository: https://github.com/raishish/arithmetic-interp.

Citation

If you would like to cite this work, please use the following BibTeX entry:

@article{rai2024arithmetic-perf-length-generalization,
  title={How do large language models perform arithmetic operations?},
  author={Rai, Ashish and Peddaputha, Akash and Gupta, Aman},
  year={2024},
  month={Dec},
  url={https://raishish.github.io/2024/12/02/llm-arithmetic-interp.html}
}